Gradient-Based Optimal Control

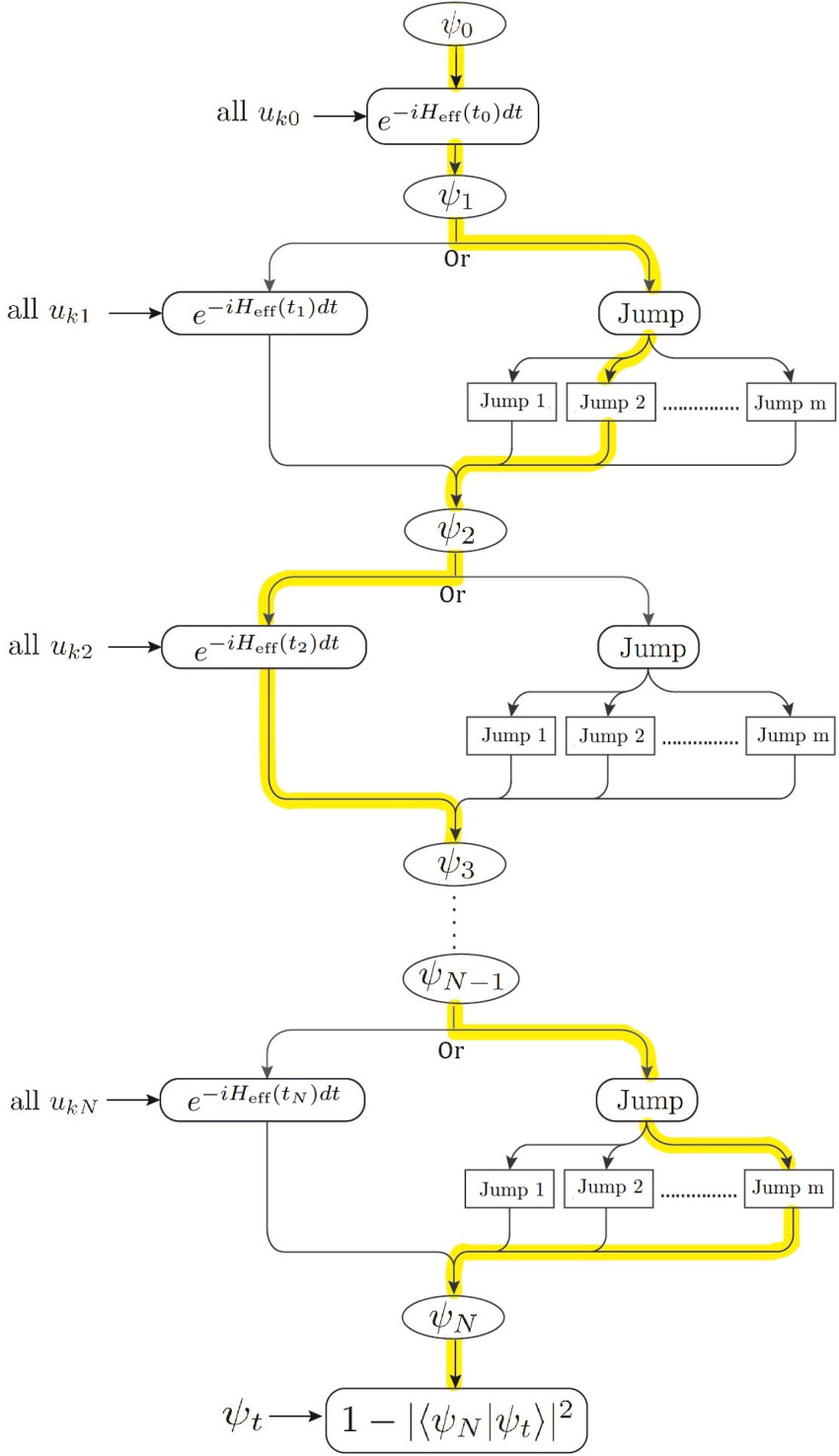
We present a gradient-based optimal-control technique for open quantum systems that utilizes quantum trajectories to simulate the quantum dynamics during optimization. Using trajectories allows for optimizing open systems with less computational cost than the regular density matrix approaches in most realistic optimization problems. We introduce an improved-sampling algorithm which minimizes the number of trajectories needed per optimization iteration. Together with employing stochastic gradient descent techniques, this reduces the complexity of optimizing many realistic open quantum systems to the complexity encountered with closed systems. Our optimizer harnesses automatic differentiation to provide flexibility in optimization and to suit the different constraints and diverse parameter regimes of real-life experiments. We utilize the optimizer in a variety of applications to demonstrate how the use of quantum trajectories significantly reduces the computation complexity while achieving a multitude of simultaneous optimization targets. Demonstrated targets include high state-transfer fidelities despite dissipation, faster gate times, and maximization of qubit-readout fidelity while maintaining the quantum nondemolition nature of the measurement and allowing for subsequent fast resonator reset. DOI 10.1103/PhysRevA.99.052327

Mohamed Abdelhafez, David I. Schuster, and Jens Koch